Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 200, pp. 1-7.
Existence and multiplicity of solutions for Dirichlet problems
involving nonlinearities with arbitrary growth
Giovanni Anello, Francesco Tulone
Abstract:
In this article we study the existence and multiplicity of solutions
for the Dirichlet problem
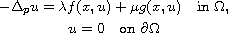
where
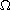 is a bounded domain in
is a bounded domain in
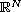 ,
,
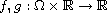 are Caratheodory functions,
and
are Caratheodory functions,
and
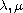 are nonnegative parameters. We impose no growth condition
at
are nonnegative parameters. We impose no growth condition
at
 on the nonlinearities f,g. A corollary to our main result
improves an existence result recently obtained by Bonanno via a critical point
theorem for
on the nonlinearities f,g. A corollary to our main result
improves an existence result recently obtained by Bonanno via a critical point
theorem for
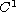 functionals which do not satisfy the usual sequential weak
lower semicontinuity property.
functionals which do not satisfy the usual sequential weak
lower semicontinuity property.
Submitted May 20, 2014. Published September 26, 2014.
Math Subject Classifications: 35J20, 35J25.
Key Words: Existence and multiplicity of solutions; Dirichlet problem;
growth condition; critical point theorem.
Show me the PDF file (216 KB),
TEX file, and other files for this article.
| |
Giovanni Anello
Department of Mathematics and Computer Science
Messina University
Viale F. Stagno D'Alcontres 31, 98166, Messina, Italy
email: ganello@unime.it
|
|---|
 |
Francesco Tulone
Department of Mathematics and Computer Science
Palermo University
Via Archirafi 34, 90123, Palermo, Italy
email: francesco.tulone@unipa.it
|
|---|
Return to the EJDE web page
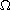 is a bounded domain in
is a bounded domain in
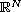 ,
,
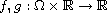 are Caratheodory functions,
and
are Caratheodory functions,
and
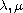 are nonnegative parameters. We impose no growth condition
at
are nonnegative parameters. We impose no growth condition
at
 on the nonlinearities f,g. A corollary to our main result
improves an existence result recently obtained by Bonanno via a critical point
theorem for
on the nonlinearities f,g. A corollary to our main result
improves an existence result recently obtained by Bonanno via a critical point
theorem for
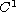 functionals which do not satisfy the usual sequential weak
lower semicontinuity property.
functionals which do not satisfy the usual sequential weak
lower semicontinuity property.
