In this article, we consider the evolution model
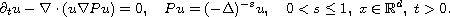
We show that when
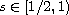 ,
,
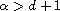 ,
,
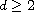 , the equation
has a unique local in time solution for any initial data in
, the equation
has a unique local in time solution for any initial data in
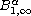 .
Moreover, in the critical case
.
Moreover, in the critical case
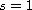 ,
the solution exists in
,
the solution exists in
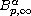 ,
,
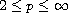 ,
,
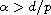 ,
,
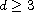 .
.
Xuhuan Zhou, Weiliang Xiao, Jiecheng Chen
Abstract:
In this article, we consider the evolution model
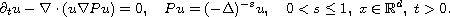
We show that when
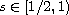 ,
,
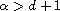 ,
,
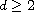 , the equation
has a unique local in time solution for any initial data in
, the equation
has a unique local in time solution for any initial data in
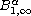 .
Moreover, in the critical case
.
Moreover, in the critical case
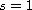 ,
the solution exists in
,
the solution exists in
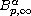 ,
,
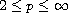 ,
,
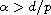 ,
,
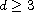 .
.
Submitted April 10, 2014. Published September 23, 2014.
Math Subject Classifications: 35K55, 35K65, 76S05.
Key Words: Fractional porous medium equation; mean field equation;
local solution; Besov space.
Show me the PDF file (252 KB), TEX file, and other files for this article.
 |
Xuhuan Zhou Department of Mathematics, Zhejiang University 310027 Hangzhou, China email: zhouxuhuan@163.com |
|---|---|
 |
Weiliang Xiao Department of Mathematics, Zhejiang University 310027 Hangzhou, China email: xwltc123@163.com |
 |
Jiecheng Chen Department of Mathematics, Zhejiang Normal University 321004 Jinhua, China email: jcchen@zjnu.edu.cn |
Return to the EJDE web page