Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 198, pp. 1-17.
Entropy solutions for nonlinear degenerate elliptic-parabolic-hyperbolic
problems
Ning Su, Li Zhang
Abstract:
We consider the nonlinear degenerate elliptic-parabolic-hyperbolic equation
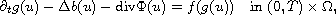
where g and b are nondecreasing continuous functions,
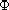 is vectorial and continuous, and f is Lipschitz continuous.
We prove the existence, comparison and uniqueness of entropy solutions
for the associated initial-boundary-value problem where
is vectorial and continuous, and f is Lipschitz continuous.
We prove the existence, comparison and uniqueness of entropy solutions
for the associated initial-boundary-value problem where
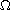 is a
bounded domain in
is a
bounded domain in
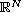 .
For the associated initial-value problem where
.
For the associated initial-value problem where
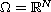 ,
,
 ,
the existence of entropy solutions is proved.
Moreover, for the case when
,
the existence of entropy solutions is proved.
Moreover, for the case when
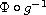 is locally Holder continuous
of order
is locally Holder continuous
of order
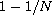 ,
and
,
and
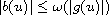 ,
where
,
where
 is nondecreasing continuous with
is nondecreasing continuous with
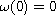 ,
we can prove the
,
we can prove the
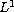 -contraction
principle, and hence the uniqueness.
-contraction
principle, and hence the uniqueness.
Submitted December 6, 2013. Published September 23, 2014.
Math Subject Classifications: 35J70, 35K65, 35L80.
Key Words: Nonlinear evolution equation; degenerate equation; entropy solution;
existence; uniqueness.
Show me the PDF file (279 KB),
TEX file, and other files for this article.
 |
Ning Su
Department of Mathematical Sciences
Tsinghua University
Beijing 100084, China
email: nsu@math.tsinghua.edu.cn
|
|---|
 |
Li Zhang
Department of Mathematical Sciences
Tsinghua University
Beijing 100084, China
email: zhli25@163.com
|
|---|
Return to the EJDE web page
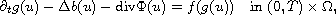
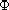 is vectorial and continuous, and f is Lipschitz continuous.
We prove the existence, comparison and uniqueness of entropy solutions
for the associated initial-boundary-value problem where
is vectorial and continuous, and f is Lipschitz continuous.
We prove the existence, comparison and uniqueness of entropy solutions
for the associated initial-boundary-value problem where
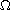 is a
bounded domain in
is a
bounded domain in
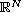 .
For the associated initial-value problem where
.
For the associated initial-value problem where
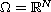 ,
,
 ,
the existence of entropy solutions is proved.
Moreover, for the case when
,
the existence of entropy solutions is proved.
Moreover, for the case when
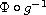 is locally Holder continuous
of order
is locally Holder continuous
of order
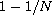 ,
and
,
and
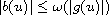 ,
where
,
where
 is nondecreasing continuous with
is nondecreasing continuous with
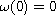 ,
we can prove the
,
we can prove the
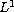 -contraction
principle, and hence the uniqueness.
-contraction
principle, and hence the uniqueness.

