Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 189, pp. 1-21.
Homogenization of geological fissured systems with curved non-periodic cracks
Fernando A. Morales
Abstract:
We analyze the steady fluid flow in a porous medium containing a network
of thin fissures of width
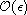 ,
generated by the rigid
translation of continuous piecewise
,
generated by the rigid
translation of continuous piecewise
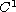 functions in a fixed direction.
The phenomenon is modeled in mixed variational formulation, using the
stationary Darcy's law and coefficients of low resistance
functions in a fixed direction.
The phenomenon is modeled in mixed variational formulation, using the
stationary Darcy's law and coefficients of low resistance
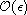 on the network. The singularities are removed by asymptotic analysis as
on the network. The singularities are removed by asymptotic analysis as
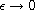 which yields an analogous system hosting only tangential
flow in the fissures. Finally the fissures are collapsed into two dimensional
manifolds.
which yields an analogous system hosting only tangential
flow in the fissures. Finally the fissures are collapsed into two dimensional
manifolds.
Submitted September 7, 2013. Published September 11, 2014.
Math Subject Classifications: 35F15, 80M40, 76S99, 35B25.
Key Words: Fissured media; tangential flow; interface geometry;
coupled Darcy flow system; upscaling; mixed formulation.
Show me the PDF file (471 KB),
TEX file, and other files for this article.
 |
Fernando A. Morales
Escuela de Matemáticas
Universidad Nacional de Colombia
Sede Medellín, Colombia
email: famoralesj@unal.edu.co
|
|---|
Return to the EJDE web page
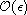 ,
generated by the rigid
translation of continuous piecewise
,
generated by the rigid
translation of continuous piecewise
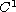 functions in a fixed direction.
The phenomenon is modeled in mixed variational formulation, using the
stationary Darcy's law and coefficients of low resistance
functions in a fixed direction.
The phenomenon is modeled in mixed variational formulation, using the
stationary Darcy's law and coefficients of low resistance
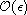 on the network. The singularities are removed by asymptotic analysis as
on the network. The singularities are removed by asymptotic analysis as
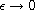 which yields an analogous system hosting only tangential
flow in the fissures. Finally the fissures are collapsed into two dimensional
manifolds.
which yields an analogous system hosting only tangential
flow in the fissures. Finally the fissures are collapsed into two dimensional
manifolds.
