Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 181, pp. 1-12.
Existence of infinitely many solutions for nonlinear Neumann problems
with indefinite coefficients
Daisuke Naimen
Abstract:
We consider the nonlinear Neumann boundary-value problem
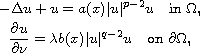
where
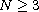 and
and
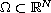 is a bounded domain
with smooth boundary. We suppose a and b are possibly sign-changing
functions in
is a bounded domain
with smooth boundary. We suppose a and b are possibly sign-changing
functions in
 and on
and on
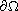 respectively.
Under some additional assumptions on a and b, we show that there
are infinitely many solutions for sufficiently small
respectively.
Under some additional assumptions on a and b, we show that there
are infinitely many solutions for sufficiently small
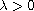 if
if
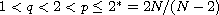 . When
. When
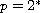 , we use the concentration compactness
argument to ensure the PS condition for the associated functional.
We also consider a general problem including the supercritical case and
obtain the existence of infinitely many solutions.
, we use the concentration compactness
argument to ensure the PS condition for the associated functional.
We also consider a general problem including the supercritical case and
obtain the existence of infinitely many solutions.
Submitted May 30, 2014. Published August 27, 2014.
Math Subject Classifications: 35J20, 35J60, 35J65.
Key Words: Nonlinear Neumann; elliptic; variational method; critical point.
Show me the PDF file (258 KB),
TEX file, and other files for this article.
 |
Daisuke Naimen
Faculty of Science, Graduate School of Science
Osaka City University
3-3-138 Sugimoto Sumiyoshi-ku, Osaka-shi
Osaka 558-8585, Japan
email: d12sax0J51@ex.media.osaka-cu.ac.jp
|
|---|
Return to the EJDE web page
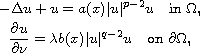
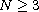 and
and
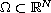 is a bounded domain
with smooth boundary. We suppose a and b are possibly sign-changing
functions in
is a bounded domain
with smooth boundary. We suppose a and b are possibly sign-changing
functions in
 and on
and on
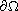 respectively.
Under some additional assumptions on a and b, we show that there
are infinitely many solutions for sufficiently small
respectively.
Under some additional assumptions on a and b, we show that there
are infinitely many solutions for sufficiently small
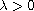 if
if
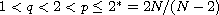 . When
. When
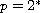 , we use the concentration compactness
argument to ensure the PS condition for the associated functional.
We also consider a general problem including the supercritical case and
obtain the existence of infinitely many solutions.
, we use the concentration compactness
argument to ensure the PS condition for the associated functional.
We also consider a general problem including the supercritical case and
obtain the existence of infinitely many solutions.
