Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 177, pp. 1-13.
Global attractivity for nonlinear differential
equations with a nonlocal term
Boumediene Abdellaoui, Tarik Mohamed Touaoula
Abstract:
In this article we analyze the dynamics of the problem
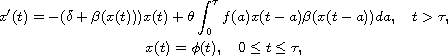
where
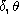 are positive constants, and
are positive constants, and
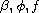 are positives continuous functions.
The main results obtained in this paper are the following:
(1) Using the Laplace transform, we prove the global asymptotic
stability of the trivial steady state.
(2) Under some additional hypotheses on the data and by constructing
a Lyapunov functional, we show the asymptotic stability of the
positive steady state.
We conclude by applying our results to mathematical models of
hematopoieses and Nicholson's blowflies.
are positives continuous functions.
The main results obtained in this paper are the following:
(1) Using the Laplace transform, we prove the global asymptotic
stability of the trivial steady state.
(2) Under some additional hypotheses on the data and by constructing
a Lyapunov functional, we show the asymptotic stability of the
positive steady state.
We conclude by applying our results to mathematical models of
hematopoieses and Nicholson's blowflies.
Submitted June 26, 2014. Published August 15, 2014.
Math Subject Classifications: 34K20, 92C37.
Key Words: Global stability; Lyapunov function; asymptotic analysis;
Laplace transform, Nicholson's blowflies model.
Show me the PDF file (262 KB),
TEX file, and other files for this article.
 |
Boumediene Abdellaoui
Laboratoire d'Analyse Nonlinéaire et Mathématiques Appliquées
Département de Mathématiques
Université Abou Bakr Belkaid
Tlemcen, Tlemcen 13000, Algeria
email: boumediene.abdellaoui@uam.es
|
|---|
 |
Tarik Mohamed Touaoula
Laboratoire d'Analyse Nonlinéaire et Mathématiques Appliquées
Département de Mathématiques
Université Abou Bakr Belkaid
Tlemcen, Tlemcen 13000, Algeria
email: touaoula_tarik@yahoo.fr, tarik.touaoula@univ-tlemcen.dz
|
|---|
Return to the EJDE web page
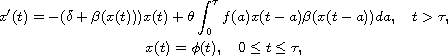
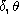 are positive constants, and
are positive constants, and
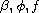 are positives continuous functions.
The main results obtained in this paper are the following:
(1) Using the Laplace transform, we prove the global asymptotic
stability of the trivial steady state.
(2) Under some additional hypotheses on the data and by constructing
a Lyapunov functional, we show the asymptotic stability of the
positive steady state.
We conclude by applying our results to mathematical models of
hematopoieses and Nicholson's blowflies.
are positives continuous functions.
The main results obtained in this paper are the following:
(1) Using the Laplace transform, we prove the global asymptotic
stability of the trivial steady state.
(2) Under some additional hypotheses on the data and by constructing
a Lyapunov functional, we show the asymptotic stability of the
positive steady state.
We conclude by applying our results to mathematical models of
hematopoieses and Nicholson's blowflies.

