Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 175, pp. 1-10.
Three-point third-order problems with a sign-changing nonlinear term
Johnny Henderson, Nickolai Kosmatov
Abstract:
In this article we study a well-known boundary value problem
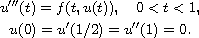
With
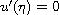 in place of
in place of
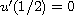 ,
many authors studied the existence
of positive solutions of both the positone problems with
,
many authors studied the existence
of positive solutions of both the positone problems with
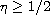 and
the semi-positone problems for
and
the semi-positone problems for
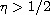 .
It is well-known that the standard
method successfully applied to the semi-positone problem with
.
It is well-known that the standard
method successfully applied to the semi-positone problem with
 does not work for
does not work for
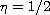 in the same setting. We treat the latter as a
problem with a sign-changing term rather than a semi-positone problem.
We apply Krasnosel'skii's fixed point theorem [4] to obtain positive solutions.
in the same setting. We treat the latter as a
problem with a sign-changing term rather than a semi-positone problem.
We apply Krasnosel'skii's fixed point theorem [4] to obtain positive solutions.
Submitted June 10, 2014. Published August 14, 2014.
Math Subject Classifications: 34B15, 34B16, 34B18.
Key Words: Green's function; fixed point theorem; positive solutions;
third-order boundary-value problem.
Show me the PDF file (213 KB),
TEX file, and other files for this article.
 |
Johnny Henderson
Department of Mathematics
Baylor University
Waco, TX 76798-7328, USA
email: Johnny_Henderson@baylor.edu
|
|---|
 |
Nickolai Kosmatov
Department of Mathematics and Statistics
University of Arkansas at Little Rock
Little Rock, AR 72204-1099, USA
email: nxkosmatov@ualr.edu
|
|---|
Return to the EJDE web page
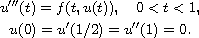
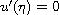 in place of
in place of
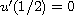 ,
many authors studied the existence
of positive solutions of both the positone problems with
,
many authors studied the existence
of positive solutions of both the positone problems with
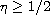 and
the semi-positone problems for
and
the semi-positone problems for
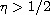 .
It is well-known that the standard
method successfully applied to the semi-positone problem with
.
It is well-known that the standard
method successfully applied to the semi-positone problem with
 does not work for
does not work for
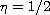 in the same setting. We treat the latter as a
problem with a sign-changing term rather than a semi-positone problem.
We apply Krasnosel'skii's fixed point theorem [4] to obtain positive solutions.
in the same setting. We treat the latter as a
problem with a sign-changing term rather than a semi-positone problem.
We apply Krasnosel'skii's fixed point theorem [4] to obtain positive solutions.

