Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 173, pp. 1-13.
Oscillation criteria for odd-order nonlinear
differential equations with advanced and delayed arguments
Ethiraju Thandapani, Sankarappan Padmavathy, Sandra Pinelas
Abstract:
This article presents oscillation criteria for n-th order nonlinear
neutral mixed type differential equations of the form
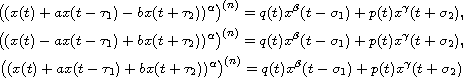
where n is an odd positive integer, a and b are nonnegative
constants,
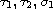 and
and
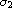 are positive
real constants,
are positive
real constants,
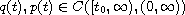 and
and
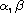 and
and
 are ratios of odd positive integers with
are ratios of odd positive integers with
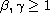 .
Some examples are provided to illustrate the main results.
.
Some examples are provided to illustrate the main results.
Submitted March 14, 2014. Published August 14, 2014.
Math Subject Classifications: 34C15.
Key Words: Oscillation; odd order; neutral differential equation; mixed type.
Show me the PDF file (241 KB),
TEX file, and other files for this article.
 |
Ethiraju Thandapani
Ramanujan Institute for Advanced Study in Mathematics
University of Madras, Chennai 600 005, India
email: ethandapani@yahoo.co.in
|
|---|
 |
Sankarappan Padmavathy
Ramanujan Institute for Advanced Study in Mathematics
University of Madras, Chennai 600 005, India
|
|---|
 |
Sandra Pinelas
Academia Militar
Departamento de Ciências Exactas e Naturais
Av. Conde Castro Guimarães, 2720-113 Amadora, Portugal
email: sandra.pinelas@gmail.com
|
|---|
Return to the EJDE web page
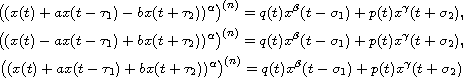
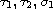 and
and
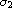 are positive
real constants,
are positive
real constants,
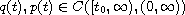 and
and
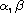 and
and
 are ratios of odd positive integers with
are ratios of odd positive integers with
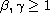 .
Some examples are provided to illustrate the main results.
.
Some examples are provided to illustrate the main results.


