In this article, we establish the multiplicity of positive weak solution for the quasilinear elliptic equation
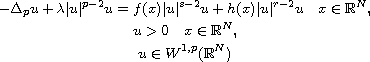
We show how the shape of the graph of f affects the number of positive solutions. Our results extend the corresponding results in [21].
Honghui Yin, Zuodong Yang
Abstract:
In this article, we establish the multiplicity of positive weak solution for
the quasilinear elliptic equation
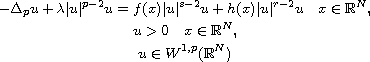
We show how the shape of the graph of f affects the number of
positive solutions. Our results extend the corresponding results
in [21].
Submitted August 4, 2013. Published January 10, 2014.
Math Subject Classifications: 35J62, 35J50, 35J92.
Key Words: Nehari manifold; quasilinear; positive solution; (PS)-sequence.
Show me the PDF file (326 KB), TEX file, and other files for this article.
| Honghui Yin Institute of Mathematics, School of Mathematical Sciences Nanjing Normal University Jiangsu Nanjing 210023, China email: yinhh771109@163.com | |

| Zuodong Yang Institute of Mathematics, School of Mathematical Sciences Nanjing Normal University Jiangsu Nanjing 210023, China email: zdyang_jin@263.net |
Return to the EJDE web page