Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 168, pp. 1-9.
Existence and non-existence of global solutions for a semilinear heat
equation on a general domain
Miguel Loayza, Crislene S. da Paixao
Abstract:
We consider the parabolic problem
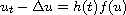 in
in
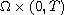 with a Dirichlet condition on the boundary
and
with a Dirichlet condition on the boundary
and
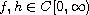 .
The initial data is assumed in the space
.
The initial data is assumed in the space
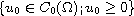 , where
, where
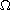 is a either bounded
or unbounded domain. We find conditions that guarantee the global
existence (or the blow up in finite time) of nonnegative solutions.
is a either bounded
or unbounded domain. We find conditions that guarantee the global
existence (or the blow up in finite time) of nonnegative solutions.
Submitted May 27, 2014. Published July 31, 2014.
Math Subject Classifications: 35K58, 35B33, 35B44.
Key Words: Parabolic equation; blow up; global solution.
Show me the PDF file (235 KB),
TEX file, and other files for this article.
 |
Miguel Loayza
Departamento de Matemática
Universidade Federal de Pernambuco - UFPE
50740-540, Recife, PE, Brazil
email: miguel@dmat.ufpe.br
|
|---|
 |
Crislene S. da Paixão
Departamento de Matemática
Universidade Federal de Pernambuco - UFPE
50740-540, Recife, PE, Brazil
email: crisspx@gmail.com
|
|---|
Return to the EJDE web page
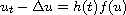 in
in
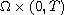 with a Dirichlet condition on the boundary
and
with a Dirichlet condition on the boundary
and
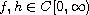 .
The initial data is assumed in the space
.
The initial data is assumed in the space
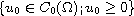 , where
, where
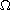 is a either bounded
or unbounded domain. We find conditions that guarantee the global
existence (or the blow up in finite time) of nonnegative solutions.
is a either bounded
or unbounded domain. We find conditions that guarantee the global
existence (or the blow up in finite time) of nonnegative solutions.

