Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 166, pp. 1-23.
Solvability of an optimal control problem in coefficients for ill-posed
elliptic boundary-value problems
Ciro D'Apice, Umberto De Maio, Peter I. Kogut, Rosanna Manzo
Abstract:
We study an optimal control problem (OCP) associated to a linear elliptic
equation
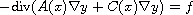 .
The characteristic feature of this control object is the fact that the
matrix
.
The characteristic feature of this control object is the fact that the
matrix
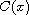 is skew-symmetric and belongs to
is skew-symmetric and belongs to
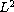 -space (rather
than
-space (rather
than
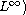 .
We adopt a symmetric
positive defined matrix
.
We adopt a symmetric
positive defined matrix
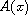 as control in
as control in
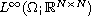 .
In spite of the fact that the equations of this type can exhibit non-uniqueness
of weak solutions, we prove that the corresponding OCP, under rather general
assumptions on the class of admissible controls, is well-posed and admits a
nonempty set of solutions. The main trick we apply to the proof of the existence
result is the approximation of the original OCP by regularized OCPs in perforated
domains with fictitious boundary controls on the holes.
.
In spite of the fact that the equations of this type can exhibit non-uniqueness
of weak solutions, we prove that the corresponding OCP, under rather general
assumptions on the class of admissible controls, is well-posed and admits a
nonempty set of solutions. The main trick we apply to the proof of the existence
result is the approximation of the original OCP by regularized OCPs in perforated
domains with fictitious boundary controls on the holes.
Submitted May 5, 2014. Published July 30, 2014.
Math Subject Classifications: 49J20, 35J57, 49J45, 35J75.
Key Words: Elliptic equation; control in coefficients; variational convergence;
fictitious control.
Show me the PDF file (376 KB),
TEX file, and other files for this article.
 |
Ciro D'Apice
Department of Information Engineering
Electrical Engineering and Applied Mathematics
University of Salerno, Via Giovanni Paolo II
132, 84084 Fisciano, Salerno, Italy
email: cdapice@unisa.it
|
|---|
 |
Umberto De Maio
Dipartimento di Matematica e Applicazioni
R. Caccioppoli, Universitá degli Studi di Napoli
Federico II, Complesso Monte S. Angelo
via Cintia, 80126 Napoli, Italy
email: udemaio@unina.it
|
|---|
 |
Peter I. Kogut
Department of Differential Equations
Dnipropetrovsk National University
Gagarin av., 72, 49010 Dnipropetrovsk, Ukraine
email: p.kogut@i.ua
|
|---|
 |
Rosanna Manzo
Department of Information Engineering
Electrical Engineering and Applied Mathematics
University of Salerno, Via Giovanni Paolo II
132, 84084 Fisciano, Salerno, Italy
email: rmanzo@unisa.it
|
|---|
Return to the EJDE web page
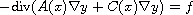 .
The characteristic feature of this control object is the fact that the
matrix
.
The characteristic feature of this control object is the fact that the
matrix
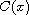 is skew-symmetric and belongs to
is skew-symmetric and belongs to
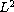 -space (rather
than
-space (rather
than
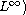 .
We adopt a symmetric
positive defined matrix
.
We adopt a symmetric
positive defined matrix
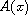 as control in
as control in
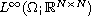 .
In spite of the fact that the equations of this type can exhibit non-uniqueness
of weak solutions, we prove that the corresponding OCP, under rather general
assumptions on the class of admissible controls, is well-posed and admits a
nonempty set of solutions. The main trick we apply to the proof of the existence
result is the approximation of the original OCP by regularized OCPs in perforated
domains with fictitious boundary controls on the holes.
.
In spite of the fact that the equations of this type can exhibit non-uniqueness
of weak solutions, we prove that the corresponding OCP, under rather general
assumptions on the class of admissible controls, is well-posed and admits a
nonempty set of solutions. The main trick we apply to the proof of the existence
result is the approximation of the original OCP by regularized OCPs in perforated
domains with fictitious boundary controls on the holes.



