Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 155, pp. 1-21.
Existence of positive solutions for p(x)-Laplacian
equations with a singular nonlinear term
Jingjing Liu, Qihu Zhang, Chunshan Zhao
Abstract:
In this article, we study the existence of positive solutions
for the p(x)-Laplacian Dirichlet problem
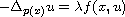
in a bounded domain
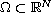 .
The singular nonlinearity term f is allowed to be either
.
The singular nonlinearity term f is allowed to be either
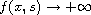 , or
, or
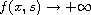 as
as
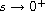 for each
for each
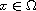 .
Our main results generalize the results
in [15] from constant exponents to variable exponents. In particular,
we give the asymptotic behavior of solutions of a simpler equation which is
useful for finding supersolutions of differential equations with variable
exponents, which is of independent interest.
.
Our main results generalize the results
in [15] from constant exponents to variable exponents. In particular,
we give the asymptotic behavior of solutions of a simpler equation which is
useful for finding supersolutions of differential equations with variable
exponents, which is of independent interest.
Submitted July 2, 2013. Published July 7, 2014.
Math Subject Classifications: 35J25, 35J65, 35J70.
Key Words: p(x)-Laplacian; singular nonlinear term; sub-supersolution method.
Show me the PDF file (335 KB),
TEX file, and other files for this article.
 |
Jingjing Liu
College of Mathematics and Information Science
Zhengzhou University of Light Industry
Zhengzhou, Henan 450002, China
email: jingjing830306@163.com
|
|---|
 |
Qihu Zhang (corresponding author)
College of Mathematics and Information Science
Zhengzhou University of Light Industry
Zhengzhou, Henan 450002, China
email:zhangqihu@yahoo.com, zhangqh1999@yahoo.com.cn
|
|---|
 |
Chunshan Zhao
Department of Mathematical Sciences
Georgia Southern University
Statesboro, GA 30460, USA
email: czhao@GeorgiaSouthern.edu
|
|---|
Return to the EJDE web page
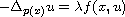
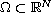 .
The singular nonlinearity term f is allowed to be either
.
The singular nonlinearity term f is allowed to be either
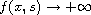 , or
, or
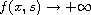 as
as
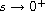 for each
for each
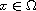 .
Our main results generalize the results
in [15] from constant exponents to variable exponents. In particular,
we give the asymptotic behavior of solutions of a simpler equation which is
useful for finding supersolutions of differential equations with variable
exponents, which is of independent interest.
.
Our main results generalize the results
in [15] from constant exponents to variable exponents. In particular,
we give the asymptotic behavior of solutions of a simpler equation which is
useful for finding supersolutions of differential equations with variable
exponents, which is of independent interest.


