Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 150, pp. 1-13.
Multiple solutions for Schrodinger-Maxwell systems with
unbounded and decaying radial potentials
Fangfang Liao, Xiaoping Wang, Zhigang Liu
Abstract:
This article concerns the nonlinear Schrodinger-Maxwell system
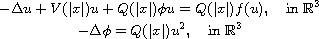
where V and Q are unbounded and decaying radial. Under suitable
assumptions on nonlinearity f(u), we establish the existence of
nontrivial solutions and a sequence of high energy solutions in
weighted Sobolev space via Mountain Pass Theorem and symmetric
Mountain Pass Theorem.
Submitted March 14, 2014. Published June 27, 2014.
Math Subject Classifications: 35J20, 35J60.
Key Words: Schrodinger-Maxwell system; unbounded or decaying potential;
weighted Sobolev space; mountain pass theorem
Show me the PDF file (245 KB),
TEX file, and other files for this article.
 |
Fangfang Liao
School of Mathematics and Statistics, Central South University
Changsha, 410083, Hunan, China.
Department of Mathematics, Xiangnan University
Chenzhou, 423000, Hunan, China
email: liaofangfang1981@126.com
|
|---|
 |
Xiaoping Wang
Department of Mathematics, Xiangnan University
Chenzhou, 423000, Hunan, China
email: wxp31415@163.com
|
|---|
 |
Zhigang Liu
Department of Mathematics, Xiangnan University
Chenzhou, 423000, Hunan, China
email: liuzg22@sina.com
|
|---|
Return to the EJDE web page