Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 15, pp. 1-22.
Lack of coercivity for N-Laplace equation with critical
exponential nonlinearities in a bounded domain
Sarika Goyal, Konijeti Sreenadh
Abstract:
In this article, we study the existence and multiplicity of
non-negative solutions of the
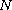 -Laplacian equation
-Laplacian equation
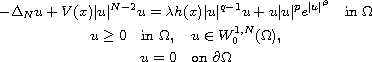
where
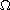 is a bounded domain in
is a bounded domain in
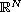 ,
,
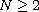 ,
,
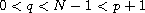 ,
,
![$\beta\in (1,\frac{N}{N-1}]$](gifs/ag.gif) and
and
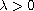 . By
minimization on a suitable subset of the Nehari manifold, and using
fiber maps, we find conditions on
. By
minimization on a suitable subset of the Nehari manifold, and using
fiber maps, we find conditions on
 ,
,
 for the existence and multiplicity of solutions, when
for the existence and multiplicity of solutions, when
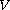 and
and
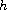 are sign
changing and unbounded functions.
are sign
changing and unbounded functions.
Submitted May 23, 2013. Published January 8, 2014.
Math Subject Classifications: 35J35, 35J60, 35J92.
Key Words: Quasilinear problem; critical exponent;
Trudinger-Moser embedding; sign-changing weight function.
Show me the PDF file (338 KB),
TEX file, and other files for this article.
 |
Sarika Goyal
Department of Mathematics
Indian Institute of Technology Delhi
Hauz Khaz, New Delhi-16, India
email: sarika1.iitd@gmail.com}
|
|---|
 |
Konijeti Sreenadh
Department of Mathematics
Indian Institute of Technology Delhi
Hauz Khaz, New Delhi-16, India
email: sreenadh@maths.iitd.ac.in
|
|---|
Return to the EJDE web page
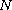 -Laplacian equation
-Laplacian equation
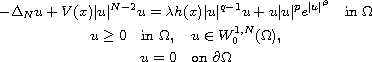
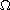 is a bounded domain in
is a bounded domain in
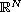 ,
,
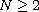 ,
,
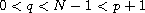 ,
,
![$\beta\in (1,\frac{N}{N-1}]$](gifs/ag.gif) and
and
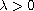 . By
minimization on a suitable subset of the Nehari manifold, and using
fiber maps, we find conditions on
. By
minimization on a suitable subset of the Nehari manifold, and using
fiber maps, we find conditions on
 ,
,
 for the existence and multiplicity of solutions, when
for the existence and multiplicity of solutions, when
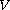 and
and
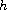 are sign
changing and unbounded functions.
are sign
changing and unbounded functions.

