Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 140, pp. 1-13.
Multiplicity of solutions for elliptic boundary value problems
Yiwei Ye, Chun-Lei Tang
Abstract:
In this article, we study the existence of infinitely many solutions
for the semilinear elliptic equation
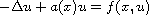 in a bounded domain of
in a bounded domain of
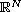
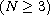 with the Dirichlet boundary conditions, where the primitive of the
nonlinearity f is either superquadratic at infinity or
subquadratic at zero.
with the Dirichlet boundary conditions, where the primitive of the
nonlinearity f is either superquadratic at infinity or
subquadratic at zero.
Submitted September 1, 2013. Published June 16, 2014.
Math Subject Classifications: 34C25, 35B38, 47J30.
Key Words: Elliptic boundary value problems; critical points;
Cerami sequence; fountain theorem; symmetric mountain pass lemma.
Show me the PDF file (261 KB),
TEX file, and other files for this article.
| |
Yiwei Ye
School of Mathematics and Statistics, Southwest University
Chongqing 400715, China
email: yeyiwei2011@126.com
|
|---|
 |
Chun-Lei Tang
School of Mathematics and Statistics, Southwest University
Chongqing 400715, China
Phone +86 23 68253135, fax +86 23 68253135
email: tangcl@swu.edu.cn
|
|---|
Return to the EJDE web page
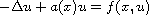 in a bounded domain of
in a bounded domain of
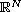
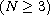 with the Dirichlet boundary conditions, where the primitive of the
nonlinearity f is either superquadratic at infinity or
subquadratic at zero.
with the Dirichlet boundary conditions, where the primitive of the
nonlinearity f is either superquadratic at infinity or
subquadratic at zero.
