In this article, we study eigenvalue problems with the p-Laplacian operator:
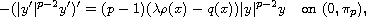
where p>1 and
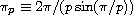 .
We show that if
.
We show that if
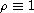 and q is single-well with transition
point
and q is single-well with transition
point
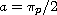 , then the second Neumann eigenvalue is greater
than or equal to the first Dirichlet eigenvalue; the equality holds
if and only if q is constant.
The same result also holds for p-Laplacian problem with
single-barrier
, then the second Neumann eigenvalue is greater
than or equal to the first Dirichlet eigenvalue; the equality holds
if and only if q is constant.
The same result also holds for p-Laplacian problem with
single-barrier
 and
and
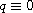 . Applying these results,
we extend and improve a result by [24]
by using finitely many eigenvalues and by generalizing the string
equation to p-Laplacian problem. Moreover, our results also extend
a result of Huang [14] on the estimate of the first instability
interval for Hill equation to single-well function q.
. Applying these results,
we extend and improve a result by [24]
by using finitely many eigenvalues and by generalizing the string
equation to p-Laplacian problem. Moreover, our results also extend
a result of Huang [14] on the estimate of the first instability
interval for Hill equation to single-well function q.
