Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 130, pp. 1-13.
Uniqueness and existence of positive solutions for singular fractional
differential equations
Nemat Nyamoradi, Tahereh Bashiri, S. Mansour Vaezpour, Dumitru Baleanu
Abstract:
In this article, we study the existence of positive solutions for the
singular fractional boundary value problem
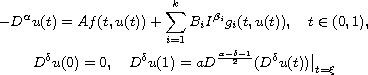
where
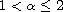 ,
,
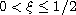 ,
,
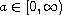 ,
,
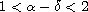 ,
,
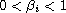 ,
,
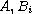 ,
,
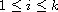 ,
are real constant,
,
are real constant,
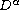 is the Riemann-Liouville fractional derivative of order
is the Riemann-Liouville fractional derivative of order
 .
By using the Banach's fixed point theorem and Leray-Schauder's alternative,
the existence of positive solutions is obtained. At last, an
example is given for illustration.
.
By using the Banach's fixed point theorem and Leray-Schauder's alternative,
the existence of positive solutions is obtained. At last, an
example is given for illustration.
Submitted August 21, 2013. Published June 6, 2014.
Math Subject Classifications: 34A08, 74H20,30E25.
Key Words: Existence of solutions; Banach’s fixed point theorem;
Leray-Schauder’s alternative.
Show me the PDF file (243 KB),
TEX file, and other files for this article.
 |
Nemat Nyamoradi
Department of Mathematics, Faculty of Sciences
Razi University, 67149 Kermanshah, Iran
email: nyamoradi@razi.ac.ir
|
|---|
 |
Tahereh Bashiri
Department of Mathematics and Computer Sciences
Amirkabir University of Technology, Tehran, Iran
email: t.bashiri@aut.ac.ir
|
|---|
 |
S. Mansour Vaezpour
Department of Mathematics and Computer Sciences
Amirkabir University of Technology, Tehran, Iran
email: vaez@aut.ac.ir
|
|---|
 |
Dumitru Baleanu
Department of Mathematics and Computer Sciences
Faculty of Art and Sciences, Cankaya University
06530 Ankara, Turkey
email: dumitru@cankaya.edu.tr
|
|---|
Return to the EJDE web page
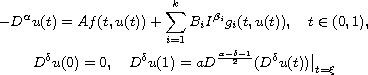
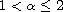 ,
,
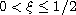 ,
,
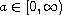 ,
,
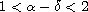 ,
,
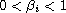 ,
,
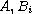 ,
,
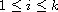 ,
are real constant,
,
are real constant,
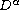 is the Riemann-Liouville fractional derivative of order
is the Riemann-Liouville fractional derivative of order
 .
By using the Banach's fixed point theorem and Leray-Schauder's alternative,
the existence of positive solutions is obtained. At last, an
example is given for illustration.
.
By using the Banach's fixed point theorem and Leray-Schauder's alternative,
the existence of positive solutions is obtained. At last, an
example is given for illustration.



