In this article, we establish a unilateral global bifurcation theorem from infinity for a class of
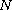 -dimensional
p-Laplacian problems.
As an application, we study the global behavior
of the components of nodal solutions of the problem
-dimensional
p-Laplacian problems.
As an application, we study the global behavior
of the components of nodal solutions of the problem
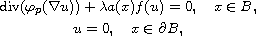
where
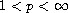 ,
,
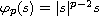 ,
,
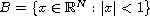 , and
, and
 is radially symmetric with
is radially symmetric with
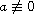 on any subset of
on any subset of
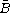 ,
,
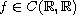 and there exist two constants
and there exist two constants
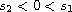 ,
such that
,
such that
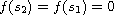 ,
and
,
and
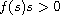 for
for
 .
Moreover, we give intervals for the parameter
.
Moreover, we give intervals for the parameter
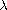 , where
the problem has multiple nodal solutions if
, where
the problem has multiple nodal solutions if
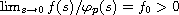 and
and
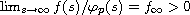 .
We use topological methods and nonlinear
analysis techniques to prove our main results.
.
We use topological methods and nonlinear
analysis techniques to prove our main results.
