Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 127, pp. 1-12.
Energy decay for elastic wave equations with critical damping
Jaqueline Luiza Horbach, Naoki Nakabayashi
Abstract:
We show that the total energy decays at the rate
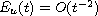 ,
as
,
as
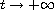 ,
for solutions to the Cauchy problem of a
linear system of elastic wave with a variable damping term.
It should be mentioned that the the critical decay satisfies
,
for solutions to the Cauchy problem of a
linear system of elastic wave with a variable damping term.
It should be mentioned that the the critical decay satisfies
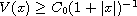 for
for
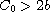 ,
where b represents
the speed of propagation of the P-wave.
,
where b represents
the speed of propagation of the P-wave.
Submitted January 17, 2014. Published May 16, 2014.
Math Subject Classifications: 35L52, 35B45, 35A25, 35B33.
Key Words: Elastic wave equation; critical damping; multiplier method;
total energy; compactly supported initial data; optimal decay.
Show me the PDF file (239 KB),
TEX file, and other files for this article.
 |
Jaqueline Luiza Horbach
Department of Mathematics
Federal University of Santa Catarina
88040-270 Florianópolis, Santa Catarina, Brazil
email: jaqueluizah@gmail.com
|
|---|
 |
Naoki Nakabayashi
Department of Mathematics
Graduate School of Education, Hiroshima University
Higashi-Hiroshima 739-8524, Japan
email: n.naoki2655@gmail.com
|
|---|
Return to the EJDE web page
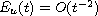 ,
as
,
as
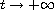 ,
for solutions to the Cauchy problem of a
linear system of elastic wave with a variable damping term.
It should be mentioned that the the critical decay satisfies
,
for solutions to the Cauchy problem of a
linear system of elastic wave with a variable damping term.
It should be mentioned that the the critical decay satisfies
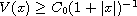 for
for
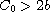 ,
where b represents
the speed of propagation of the P-wave.
,
where b represents
the speed of propagation of the P-wave.

