Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 126, pp. 1-13.
Strictly positive solutions for one-dimensional nonlinear elliptic problems
Uriel Kaufmann, Ivan Medri
Abstract:
We study the existence and nonexistence of strictly positive solutions
for the elliptic problems
 in a bounded open interval,
with zero boundary conditions, where
in a bounded open interval,
with zero boundary conditions, where
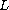 is a strongly uniformly
elliptic differential operator,
is a strongly uniformly
elliptic differential operator,
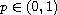 , and
, and
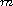 is a function
that changes sign. We also characterize the set of values
is a function
that changes sign. We also characterize the set of values
 for which the problem admits a solution, and in addition an existence
result for other nonlinearities is presented.
for which the problem admits a solution, and in addition an existence
result for other nonlinearities is presented.
Submitted June 26, 2013. Published May 14, 2014.
Math Subject Classifications: 34B15, 34B18, 35J25, 35J61.
Key Words: Elliptic one-dimensional problems; indefinite nonlinearities;
sub and supersolutions; positive solutions.
Show me the PDF file (263 KB),
TEX file, and other files for this article.
 |
Uriel Kaufmann
FaMAF, Universidad Nacional de Córdoba, (5000)
Córdoba, Argentina
email: kaufmann@mate.uncor.edu
|
|---|
 |
Iván Medri
FaMAF, Universidad Nacional de Córdoba, (5000)
Córdoba, Argentina
email: medri@mate.uncor.edu
|
|---|
Return to the EJDE web page
 in a bounded open interval,
with zero boundary conditions, where
in a bounded open interval,
with zero boundary conditions, where
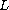 is a strongly uniformly
elliptic differential operator,
is a strongly uniformly
elliptic differential operator,
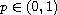 , and
, and
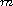 is a function
that changes sign. We also characterize the set of values
is a function
that changes sign. We also characterize the set of values
 for which the problem admits a solution, and in addition an existence
result for other nonlinearities is presented.
for which the problem admits a solution, and in addition an existence
result for other nonlinearities is presented.

