Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 125, pp. 1-11.
Growth of meromorphic solutions of higher order
linear differential equations
Lijun Wang, Huifang Liu
Abstract:
In this article, we investigate the growth of
meromorphic solutions of the differential equations
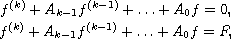
where
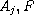
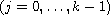 are meromorphic functions. When there
exists one dominant coefficient with lower order less than 1/2, we
obtain some estimations of the hyper order and the hyper convergence
exponent of zeros of meromorphic solutions of the above equations.
are meromorphic functions. When there
exists one dominant coefficient with lower order less than 1/2, we
obtain some estimations of the hyper order and the hyper convergence
exponent of zeros of meromorphic solutions of the above equations.
Submitted January 27, 2014. Published May 14, 2014.
Math Subject Classifications: 30D35, 39B12.
Key Words: Meromorphic function; differential equations; growth; order.
Show me the PDF file (241 KB),
TEX file, and other files for this article.
 |
Lijun Wang
College of Mathematics and Information Science
Jiangxi Normal University, Nanchang 330022, China
email: lijunwangz@163.com
|
|---|
 |
Huifang Liu
College of Mathematics and Information Science
Jiangxi Normal University, Nanchang 330022, China
email: liuhuifang73@sina.com, 925268196@qq.com
|
|---|
Return to the EJDE web page
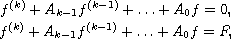
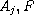
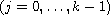 are meromorphic functions. When there
exists one dominant coefficient with lower order less than 1/2, we
obtain some estimations of the hyper order and the hyper convergence
exponent of zeros of meromorphic solutions of the above equations.
are meromorphic functions. When there
exists one dominant coefficient with lower order less than 1/2, we
obtain some estimations of the hyper order and the hyper convergence
exponent of zeros of meromorphic solutions of the above equations.

