By using the genus properties, we establish some criteria for the second-order p(t)-Laplacian system
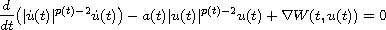
to have at least one, and infinitely many homoclinic orbits. where
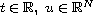 ,
,
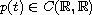 and
and
 ,
,
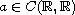 and
and
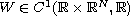 may not be periodic in t.
may not be periodic in t.
Bin Qin, Peng Chen
Abstract:
By using the genus properties, we establish some criteria
for the second-order p(t)-Laplacian system
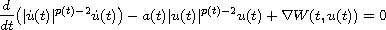
to have at least one, and infinitely many homoclinic orbits.
where
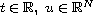 ,
,
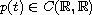 and
and
 ,
,
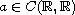 and
and
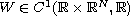 may not be periodic in t.
may not be periodic in t.
Submitted December 17, 2013. Published April 16, 2014.
Math Subject Classifications: 34C37, 58E05, 70H05.
Key Words: Homoclinic solutions; p(t)-Laplacian systems; genus.
Show me the PDF file (252 KB), TEX file, and other files for this article.
| Bin Qin College of Science, China Three Gorges University Yichang, Hubei 443002, China email: 1070751409@qq.com |
| Peng Chen College of Science, China Three Gorges University Yichang, Hubei 443002, China email: pengchen729@sina.com |
Return to the EJDE web page