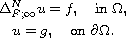Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 109, pp. 1-17.
Existence of solutions to a normalized F-infinity Laplacian equation
Hua Wang, Yijun He
Abstract:
In this article, for a continuous function F that is twice differentiable
at a point
 ,
we define the normalized F-infinity Laplacian
,
we define the normalized F-infinity Laplacian
 which is a generalization of the usual normalized
infinity Laplacian.
Then for a bounded domain
which is a generalization of the usual normalized
infinity Laplacian.
Then for a bounded domain
 ,
,
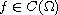 with
with
 and
and
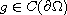 ,
we obtain existence and
uniqueness of viscosity solutions to the Dirichlet boundary-value problem
,
we obtain existence and
uniqueness of viscosity solutions to the Dirichlet boundary-value problem
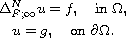
Submitted March 18, 2014. Published April 16, 2104.
Math Subject Classifications: 35D40, 35J60, 35J70
Key Words: March 18, 2014. Published April 16, 2014.
Show me the PDF file (293 KB),
TEX file, and other files for this article.
 |
Hua Wang
School of Mathematical Sciences,
Shanxi University
Taiyuan 030006, China
email: 197wang@163.com
|
|---|
 |
Yijun He
School of Mathematical Sciences,
Shanxi University
Taiyuan 030006, China
email: heyijun@sxu.edu.cn
|
|---|
Return to the EJDE web page
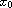 ,
we define the normalized F-infinity Laplacian
,
we define the normalized F-infinity Laplacian
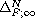 which is a generalization of the usual normalized
infinity Laplacian.
Then for a bounded domain
which is a generalization of the usual normalized
infinity Laplacian.
Then for a bounded domain
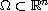 ,
,
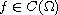 with
with
 and
and
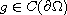 ,
we obtain existence and
uniqueness of viscosity solutions to the Dirichlet boundary-value problem
,
we obtain existence and
uniqueness of viscosity solutions to the Dirichlet boundary-value problem