This article presents a new theory on the nature of turbulence: when the Reynolds number is large, violent fully developed turbulence is due to "rough dependence on initial data" rather than chaos which is caused by "sensitive dependence on initial data"; when the Reynolds number is moderate, (often transient) turbulence is due to chaos. The key in the validation of the theory is estimating the temporal growth of the initial perturbations with the Reynolds number as a parameter. Analytically, this amounts to estimating the temporal growth of the norm of the derivative of the solution map of the Navier-Stokes equations, for which here I obtain an upper bound
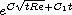 .
This bound clearly indicates that when the Reynolds
number is large, the temporal growth rate can potentially be large in
short time, i.e. rough dependence on initial data.
.
This bound clearly indicates that when the Reynolds
number is large, the temporal growth rate can potentially be large in
short time, i.e. rough dependence on initial data.
