Electron. J. Diff. Equ., Vol. 2014 (2014), No. 100, pp. 1-11.

Stability and periodicity of solutions for delay dynamic systems on time scales

Zhi-Qiang Zhu, Qi-Ru Wang

Abstract:
This article concerns the stability and periodicity of solutions to the delay dynamic system
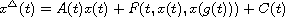
$$ x^{\triangle}(t)=A(t) x(t) + F(t, x(t), x(g(t)))+C(t) $$
on a time scale. By the inequality technique for vectors, we obtain some stability criteria for the above system. Then, by using the Horn fixed point theorem, we present some conditions under which our system is asymptotically periodic and its periodic solution is unique. In particular, the periodic solution is positive under proper assumptions.

Submitted November 17, 2013. Published April 11, 2014.
Math Subject Classifications: 34N05, 34K13, 34K20.
Key Words: Delay dynamic system; stability; periodic solution; fixed point; time scales.

Show me the PDF file (248 KB), TEX file, and other files for this article.

Zhi-Qiang Zhu
Department of Computer Science
Guangdong Polytechnic Normal University
Guangzhou 510665, China
email: z3825@163.com
Qi-Ru Wang
School of Mathematics and Computational Science
Sun Yat-Sen University
Guangzhou 510275, China
email: mcswqr@mail.sysu.edu.cn

Return to the EJDE web page