Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 09, pp. 1-20.
Boundary blow-up solutions to semilinear elliptic equations with
nonlinear gradient terms
Shufang Liu, Yonglin Xu
Abstract:
In this article we study the blow-up rate of solutions
near the boundary for the semilinear elliptic problem
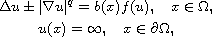
where
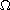 is a smooth bounded domain in
is a smooth bounded domain in
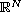 ,
and b(x) is a
nonnegative weight function which may be bounded or singular on
the boundary, and f is a regularly varying function at infinity.
The results in this article emphasize the central role played by
the nonlinear gradient term
,
and b(x) is a
nonnegative weight function which may be bounded or singular on
the boundary, and f is a regularly varying function at infinity.
The results in this article emphasize the central role played by
the nonlinear gradient term
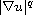 and the singular weight b(x).
Our main tools are the Karamata regular variation theory and the method of
explosive upper and lower solutions.
and the singular weight b(x).
Our main tools are the Karamata regular variation theory and the method of
explosive upper and lower solutions.
Submitted October 4, 2013. Published January 7, 2014.
Math Subject Classifications: 35J25, 35B50, 65J65.
Key Words: Boundary blow-up solutions; nonlinear gradient terms;
Karamata regular variation.
Show me the PDF file (299 KB),
TEX file, and other files for this article.
 |
Shufang Liu
Department of Mathematics
Gansu Normal University for Nationalities
Hezuo, Gansu 747000, China
email: shuxueliushufang@163.com
|
|---|
 |
Yonglin Xu
School of Mathematics and Computer Science Institute
Northwest University for Nationalities
Lanzhou, Gansu 730030, China
email: xuyonglin000@163.com
|
|---|
Return to the EJDE web page
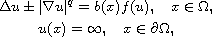
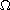 is a smooth bounded domain in
is a smooth bounded domain in
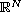 ,
and b(x) is a
nonnegative weight function which may be bounded or singular on
the boundary, and f is a regularly varying function at infinity.
The results in this article emphasize the central role played by
the nonlinear gradient term
,
and b(x) is a
nonnegative weight function which may be bounded or singular on
the boundary, and f is a regularly varying function at infinity.
The results in this article emphasize the central role played by
the nonlinear gradient term
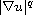 and the singular weight b(x).
Our main tools are the Karamata regular variation theory and the method of
explosive upper and lower solutions.
and the singular weight b(x).
Our main tools are the Karamata regular variation theory and the method of
explosive upper and lower solutions.

