Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 08, pp. 1-10.
Estimates on potential functions and boundary behavior
of positive solutions for sublinear Dirichlet problems
Ramzi Alsaedi, Habib Maagli, Noureddine Zeddini
Abstract:
We give global estimates on some potential of functions in a bounded domain
of the Euclidean space
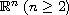 . These functions
may be singular near the boundary and are globally comparable to a product
of a power of the distance to the boundary by some particularly well behaved
slowly varying function near zero. Next, we prove the existence and uniqueness
of a positive solution for the integral equation
. These functions
may be singular near the boundary and are globally comparable to a product
of a power of the distance to the boundary by some particularly well behaved
slowly varying function near zero. Next, we prove the existence and uniqueness
of a positive solution for the integral equation
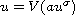 with
with
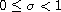 ,
where V belongs to a class of kernels that contains
in particular the potential kernel of the classical Laplacian
,
where V belongs to a class of kernels that contains
in particular the potential kernel of the classical Laplacian
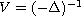 or the fractional laplacian
or the fractional laplacian
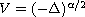 ,
,
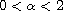 .
.
Submitted September 14, 2013. Published January 7, 2014.
Math Subject Classifications: 35R11, 35B40, 35J08.
Key Words: Green function; Dirichlet Laplacian; fractional Laplacian;
Karamata function.
Show me the PDF file (235 KB),
TEX file, and other files for this article.
 |
Ramzi Alsaedi
Department of Mathematics, College of Sciences and Arts
King Abdulaziz University, Rabigh Campus
P.O. Box 344, Rabigh 21911, Saudi Arabia
email: ramzialsaedi@yahoo.co.uk
|
|---|
 |
Habib Mâagli
Department of Mathematics, College of Sciences and Arts
King Abdulaziz University, Rabigh Campus
P.O. Box 344, Rabigh 21911, Saudi Arabia
email: habib.maagli@fst.rnu.tn
|
|---|
 |
Noureddine Zeddini
Department of Mathematics, College of Sciences and Arts
King Abdulaziz University, Rabigh Campus
P.O. Box 344, Rabigh 21911, Saudi Arabia
email: noureddine.zeddini@ipein.rnu.tn
|
|---|
Return to the EJDE web page
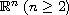 . These functions
may be singular near the boundary and are globally comparable to a product
of a power of the distance to the boundary by some particularly well behaved
slowly varying function near zero. Next, we prove the existence and uniqueness
of a positive solution for the integral equation
. These functions
may be singular near the boundary and are globally comparable to a product
of a power of the distance to the boundary by some particularly well behaved
slowly varying function near zero. Next, we prove the existence and uniqueness
of a positive solution for the integral equation
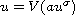 with
with
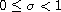 ,
where V belongs to a class of kernels that contains
in particular the potential kernel of the classical Laplacian
,
where V belongs to a class of kernels that contains
in particular the potential kernel of the classical Laplacian
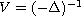 or the fractional laplacian
or the fractional laplacian
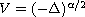 ,
,
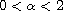 .
.


