Electron. J. Diff. Equ.,
Vol. 2014 (2014), No. 01, pp. 1-13.
Stability for trajectories of periodic evolution families in Hilbert spaces
Dorel Barbu, Joel Blot, Constantin Buse, Olivia Saierli
Abstract:
Let
 be a positive real number and let
be a positive real number and let
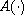 be a
be a
 -periodic
linear operator valued function on a complex Hilbert space
-periodic
linear operator valued function on a complex Hilbert space
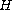 , and
let
, and
let
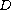 be a dense linear subspace of
be a dense linear subspace of
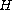 .
Let
.
Let
 be the evolution family
generated by the family
be the evolution family
generated by the family
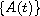 .
We prove that if the solution of the well-posed inhomogeneous
Cauchy Problem
.
We prove that if the solution of the well-posed inhomogeneous
Cauchy Problem

is bounded on
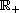 ,
for every
,
for every
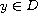 ,
and every
,
and every
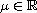 ,
by the positive constant
,
by the positive constant
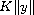 ,
,
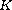 being an absolute constant, and if, in addition, for some
being an absolute constant, and if, in addition, for some
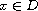 ,
the trajectory
,
the trajectory
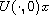 satisfies a Lipschitz condition on the interval
satisfies a Lipschitz condition on the interval
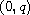 ,
then
,
then
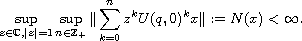
The latter discrete boundedness condition has a lot of consequences
concerning the stability of solutions of the abstract nonautonomous
system
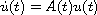 .
To our knowledge, these results are new.
In the special case, when
.
To our knowledge, these results are new.
In the special case, when
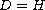 and for every
and for every
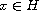 , the map
, the map
 satisfies a Lipschitz condition on the interval
satisfies a Lipschitz condition on the interval
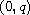 ,
the evolution family
,
the evolution family
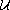 is uniformly exponentially stable.
In the autonomous case, (i.e. when
is uniformly exponentially stable.
In the autonomous case, (i.e. when
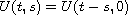 for every pair
for every pair
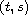 with
with
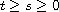 ),
the latter assumption is too restrictive.
More exactly, in this case, the semigroup
),
the latter assumption is too restrictive.
More exactly, in this case, the semigroup
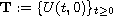 ,
is uniformly continuous.
,
is uniformly continuous.
Submitted August 23, 2013. Published January 3, 2014.
Math Subject Classifications: 47A05, 47A30, 47D06, 47A10, 35B15, 35B10.
Key Words: Periodic evolution families; uniform exponential stability;
boundedness; strongly continuous semigroup;
periodic and almost periodic functions.
Show me the PDF file (285 KB),
TEX file, and other files for this article.
 |
Dorel Barbu
West University of Timisoara, Department of Mathematics
Bd. V. Parvan No. 4, 300223-Timisoara, Romania
email: barbu@math.uvt.ro
|
|---|
 |
Joel Blot
Laboratoire SAMM EA 4543, University Paris 1
Sorbonne-Pantheon, Centre P. M. F.
90 rue de Tolbiac, 75634 Paris Cedex 13, France
email: Joel.Blot@univ-paris1.fr
|
|---|
 |
Constantin Buse
West University of Timisoara, Department of Mathematics
Bd. V. Parvan No. 4, 300223-Timisoara, Romania
email: buse@math.uvt.ro
|
|---|
 |
Olivia Saierli
Tibiscus University of Timisoara
Department of Computer Science and Applied Informatics
Str. Lascar Catargiu, No. 4-6,300559-Timisoara, Romania
email: saierli_olivia@yahoo.com
|
|---|
Return to the EJDE web page
 be a positive real number and let
be a positive real number and let
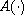 be a
be a
 -periodic
linear operator valued function on a complex Hilbert space
-periodic
linear operator valued function on a complex Hilbert space
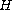 , and
let
, and
let
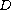 be a dense linear subspace of
be a dense linear subspace of
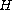 .
Let
.
Let
 be the evolution family
generated by the family
be the evolution family
generated by the family
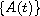 .
We prove that if the solution of the well-posed inhomogeneous
Cauchy Problem
.
We prove that if the solution of the well-posed inhomogeneous
Cauchy Problem

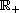 ,
for every
,
for every
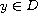 ,
and every
,
and every
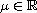 ,
by the positive constant
,
by the positive constant
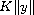 ,
,
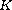 being an absolute constant, and if, in addition, for some
being an absolute constant, and if, in addition, for some
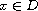 ,
the trajectory
,
the trajectory
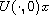 satisfies a Lipschitz condition on the interval
satisfies a Lipschitz condition on the interval
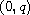 ,
then
,
then
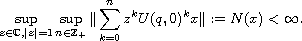
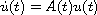 .
To our knowledge, these results are new.
In the special case, when
.
To our knowledge, these results are new.
In the special case, when
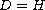 and for every
and for every
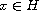 , the map
, the map
 satisfies a Lipschitz condition on the interval
satisfies a Lipschitz condition on the interval
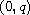 ,
the evolution family
,
the evolution family
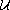 is uniformly exponentially stable.
In the autonomous case, (i.e. when
is uniformly exponentially stable.
In the autonomous case, (i.e. when
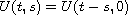 for every pair
for every pair
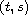 with
with
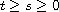 ),
the latter assumption is too restrictive.
More exactly, in this case, the semigroup
),
the latter assumption is too restrictive.
More exactly, in this case, the semigroup
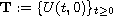 ,
is uniformly continuous.
,
is uniformly continuous.



