The global stability for a delayed HBV infection model with CTL immune response is investigated. We show that the global dynamics is determined by two sharp thresholds, basic reproduction number
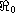 and CTL immune-response reproduction number
and CTL immune-response reproduction number
 . When
. When
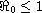 ,
the infection-free equilibrium is globally asymptotically stable, which
means that the viruses are cleared and immune is not active;
when
,
the infection-free equilibrium is globally asymptotically stable, which
means that the viruses are cleared and immune is not active;
when
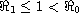 , the CTL-inactivated infection equilibrium
exists and is globally asymptotically stable, which means that CTLs immune
response would not be activated and viral infection becomes chronic;
and when
, the CTL-inactivated infection equilibrium
exists and is globally asymptotically stable, which means that CTLs immune
response would not be activated and viral infection becomes chronic;
and when
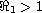 , the CTL-activated infection equilibrium exists and
is globally asymptotically stable, in this case the infection causes
a persistent CTLs immune response. Our model is formulated by
incorporating
a Cytotoxic T lymphocytes (CTLs) immune response to recent work
[Gourley, Kuang, Nagy, J. Bio. Dyn., 2(2008), 140-153]
to model the role in antiviral by attacking virus infected cells.
Our analysis provides a quantitative understandings of HBV replication
dynamics in vivo and has implications for the optimal timing of drug
treatment and immunotherapy in chronic HBV infection.
, the CTL-activated infection equilibrium exists and
is globally asymptotically stable, in this case the infection causes
a persistent CTLs immune response. Our model is formulated by
incorporating
a Cytotoxic T lymphocytes (CTLs) immune response to recent work
[Gourley, Kuang, Nagy, J. Bio. Dyn., 2(2008), 140-153]
to model the role in antiviral by attacking virus infected cells.
Our analysis provides a quantitative understandings of HBV replication
dynamics in vivo and has implications for the optimal timing of drug
treatment and immunotherapy in chronic HBV infection.

