Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 89, pp. 1-7.
Exponential dichotomy of nonautonomous periodic systems in terms of
the boundedness of certain periodic Cauchy problems
Dhaou Lassoued
Abstract:
We prove that a family of
 -periodic
continuous matrix valued
function
-periodic
continuous matrix valued
function
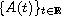 has an exponential dichotomy
with a projector
has an exponential dichotomy
with a projector
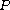 if and only if
if and only if
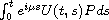 is bounded uniformly with respect to the parameter
is bounded uniformly with respect to the parameter
 and
the solution of the Cauchy operator Problem
and
the solution of the Cauchy operator Problem
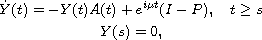
has a limit in
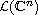 as s tends to
as s tends to
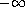 which is bounded uniformly with respect to the parameter
which is bounded uniformly with respect to the parameter
 .
Here,
.
Here,
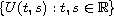 is the evolution family
generated by
is the evolution family
generated by
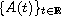 ,
,
 is a real number and q is a fixed positive number.
is a real number and q is a fixed positive number.
Submitted February 1, 2013. Published April 5, 2013.
Math Subject Classifications: 47A05, 34D09, 35B35.
Key Words: Periodic evolution families; exponential dichotomy;
boundedness.
Show me the PDF file (201 KB),
TEX file, and other files for this article.
 |
Dhaou Lassoued
Laboratoire SAMM EA4543
Université Paris 1 Panthéon-Sorbonne
centre P.M.F., 90 rue de Tolbiac
75634 Paris cedex 13, France
email: Dhaou.Lassoued@univ-paris1.fr, dhaou06@gmail.com
|
|---|
Return to the EJDE web page
 -periodic
continuous matrix valued
function
-periodic
continuous matrix valued
function
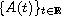 has an exponential dichotomy
with a projector
has an exponential dichotomy
with a projector
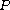 if and only if
if and only if
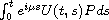 is bounded uniformly with respect to the parameter
is bounded uniformly with respect to the parameter
 and
the solution of the Cauchy operator Problem
and
the solution of the Cauchy operator Problem
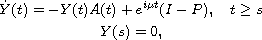
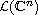 as s tends to
as s tends to
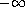 which is bounded uniformly with respect to the parameter
which is bounded uniformly with respect to the parameter
 .
Here,
.
Here,
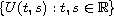 is the evolution family
generated by
is the evolution family
generated by
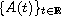 ,
,
 is a real number and q is a fixed positive number.
is a real number and q is a fixed positive number.
