Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 65, pp. 1-7.
Constant sign solutions for second-order m-point boundary-value problems
Jingping Yang
Abstract:
We will study the existence of constant sign solutions for the second-order
m-point boundary-value problem
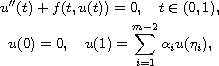
where
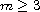 ,
,
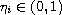 and
and
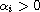 for
for
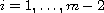 , with
, with
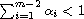 ,
we obtain that
there exist at least a positive and a negative
solution for the above problem. Our approach is based on
unilateral global bifurcation theorem.
,
we obtain that
there exist at least a positive and a negative
solution for the above problem. Our approach is based on
unilateral global bifurcation theorem.
Submitted November 8, 2012. Published March 5, 2013.
Math Subject Classifications: 34B18, 34C25.
Key Words: Constant sign solutions; eigenvalue; bifurcation methods.
Show me the PDF file (199 KB),
TEX file, and other files for this article.
Jingping Yang
Gansu Institute of Political Science and Law
Lanzhou, 730070, China
email: fuj09@lzu.cn
|
Return to the EJDE web page
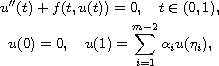
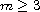 ,
,
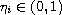 and
and
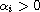 for
for
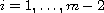 , with
, with
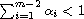 ,
we obtain that
there exist at least a positive and a negative
solution for the above problem. Our approach is based on
unilateral global bifurcation theorem.
,
we obtain that
there exist at least a positive and a negative
solution for the above problem. Our approach is based on
unilateral global bifurcation theorem.