In this article we present local
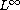 estimates for the gradient
of solutions to elliptic equations with variable exponents.
Under proper conditions on the coefficients, we prove that
estimates for the gradient
of solutions to elliptic equations with variable exponents.
Under proper conditions on the coefficients, we prove that
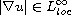
for all weak solutions of
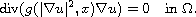
Fengping Yao
Abstract:
In this article we present local
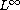 estimates for the gradient
of solutions to elliptic equations with variable exponents.
Under proper conditions on the coefficients, we prove that
estimates for the gradient
of solutions to elliptic equations with variable exponents.
Under proper conditions on the coefficients, we prove that
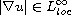
for all weak solutions of
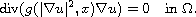
Submitted September 3, 2012. Published February 18, 2013.
Math Subject Classifications: 35J60, 35J70.
Key Words: Regularity; divergence; nonlinear; elliptic equation;
gradient; variable exponent; p(x)-Laplacian.
Show me the PDF file (220 KB), TEX file, and other files for this article.
 |
Fengping Yao Department of Mathematics, Shanghai University Shanghai 200444, China email: yfp@shu.edu.cn |
|---|
Return to the EJDE web page