Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 33, pp. 1-10.
Positive blowup solutions for some fractional systems in bounded domains
Ramzi Alsaedi
Abstract:
Using some potential theory tools and the Schauder fixed point theorem,
we prove the existence of a positive continuous weak solution
for the fractional system
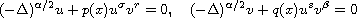
in a bounded
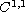 -domain D in
-domain D in
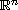
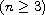 ,
subject to Dirichlet conditions, where
,
subject to Dirichlet conditions, where
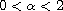 ,
,
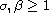 ,
,
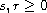 . The potential functions p,q
are nonnegative and required to satisfy some adequate hypotheses related
to the Kato class
. The potential functions p,q
are nonnegative and required to satisfy some adequate hypotheses related
to the Kato class
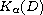 . We also investigate the global
behavior of such solution.
. We also investigate the global
behavior of such solution.
Submitted November 2, 2012. Published January 30, 2013.
Math Subject Classifications: 26A33, 34B27, 35B44, 35B09.
Key Words: Fractional nonlinear systems, Green function, positive solutions,
maximum principle.
Show me the PDF file (236 KB),
TEX file, and other files for this article.
Ramzi Alsaedi
Department of Mathematics, College of Science and Arts
King Abdulaziz University, Rabigh Campus, P. O. Box 344
Rabigh 21911, Saudi Arabia
email: ramzialsaedi@yahoo.co.uk
|
Return to the EJDE web page
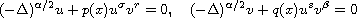
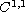 -domain D in
-domain D in
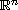
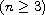 ,
subject to Dirichlet conditions, where
,
subject to Dirichlet conditions, where
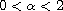 ,
,
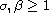 ,
,
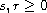 . The potential functions p,q
are nonnegative and required to satisfy some adequate hypotheses related
to the Kato class
. The potential functions p,q
are nonnegative and required to satisfy some adequate hypotheses related
to the Kato class
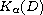 . We also investigate the global
behavior of such solution.
. We also investigate the global
behavior of such solution.