Using the Schauder fixed point theorem, we prove an existence of positive solutions for the fractional differential problem in the half line
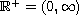 :
:
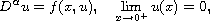
where
![$\alpha \in (1,2]$](gifs/ac.gif) and
and
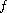 is a Borel measurable function in
is a Borel measurable function in
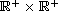 satisfying some appropriate
conditions.
satisfying some appropriate
conditions.
Habib Maagli
Abstract:
Using the Schauder fixed point theorem, we prove an existence of
positive solutions for the fractional differential problem
in the half line
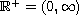 :
:
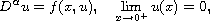
where
![$\alpha \in (1,2]$](gifs/ac.gif) and
and
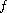 is a Borel measurable function in
is a Borel measurable function in
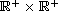 satisfying some appropriate
conditions.
satisfying some appropriate
conditions.
Submitted November 25, 2012. Published January 28, 2013.
Math Subject Classifications: 34A08.
Key Words: Riemann-Liouville fractional derivative; fixed point theorem.
Show me the PDF file (178 KB), TEX file, and other files for this article.
 |
Habib Maagli King Abdulaziz University, College of Sciences ant Arts Rabigh Campus, Department of Mathematics P.O. Box 344, Rabigh 21911, Kingdom of Saudi Arabia email: habib.maagli@fst.rnu.tn |
|---|
Return to the EJDE web page