In this work we prove the existence of solutions for the fractional differential equation

where
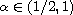 .
Assuming L is coercive at infinity we show that this equation
has at least one nontrivial solution.
.
Assuming L is coercive at infinity we show that this equation
has at least one nontrivial solution.
Cesar Torres
Abstract:
In this work we prove the existence of solutions for the
fractional differential equation

where
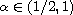 .
Assuming L is coercive at infinity we show that this equation
has at least one nontrivial solution.
.
Assuming L is coercive at infinity we show that this equation
has at least one nontrivial solution.
Submitted June 10, 2013. Published November 26, 2013.
Math Subject Classifications: 26A33, 34C37, 35A15, 35B38.
Key Words: Liouville-Weyl fractional derivative; fractional Hamiltonian systems;
critical point; variational methods.
Show me the PDF file (255 KB), TEX file, and other files for this article.
 |
César Torres Departamento de Ingeniería Matemática and Centro de Modelamiento Matemático UMR2071 CNRS-UChile, Universidad de Chile Santiago, Chile email: ctorres@dim.uchile.cl |
|---|
Return to the EJDE web page