Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 258, pp. 1-9.
A uniqueness result for an inverse problem in a space-time fractional
diffusion equation
Salih Tatar, Suleyman Ulusoy
Abstract:
Fractional (nonlocal) diffusion equations replace the integer-order
derivatives in space and time by fractional-order derivatives.
This article considers a nonlocal inverse problem and shows that
the exponents of the fractional time and space derivatives
are determined uniquely by the data
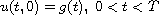 .
The uniqueness result is a theoretical background for determining
experimentally the order of many anomalous diffusion phenomena,
which are important in physics and in environmental engineering.
.
The uniqueness result is a theoretical background for determining
experimentally the order of many anomalous diffusion phenomena,
which are important in physics and in environmental engineering.
Submitted May 8, 2013. Published November 22, 2013.
Math Subject Classifications: 45K05, 35R30, 65M32.
Key Words: Fractional derivative; fractional Laplacian; weak solution;
inverse problem; Mittag-Leffler function; Cauchy problem.
Show me the PDF file (220 KB),
TEX file, and other files for this article.
 |
Salih Tatar
Department of Mathematics
Faculty of Education, Zirve University
Sahinbey, Gaziantep, 27270, Turkey
email: salih.tatar@zirve.edu.tr
http://person.zirve.edu.tr/statar/
|
|---|
 |
Süleyman Ulusoy
Department of Mathematics
Faculty of Education, Zirve University
Sahinbey, Gaziantep, 27270, Turkey
email: suleyman.ulusoy@zirve.edu.tr
http://person.zirve.edu.tr/ulusoy/
|
|---|
Return to the EJDE web page
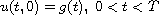 .
The uniqueness result is a theoretical background for determining
experimentally the order of many anomalous diffusion phenomena,
which are important in physics and in environmental engineering.
.
The uniqueness result is a theoretical background for determining
experimentally the order of many anomalous diffusion phenomena,
which are important in physics and in environmental engineering.

