In this article, we study the nonlocal
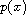 -Laplacian problem
-Laplacian problem
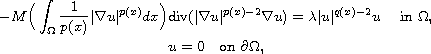
By means of variational methods and the theory of the variable exponent Sobolev spaces, we establish conditions for the existence of weak solutions.
Ghasem A. Afrouzi, Maryam Mirzapour
Abstract:
In this article, we study the nonlocal
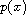 -Laplacian problem
-Laplacian problem
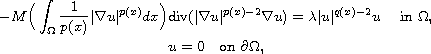
By means of variational methods and the theory of the variable
exponent Sobolev spaces, we establish conditions for the
existence of weak solutions.
Submitted August 17, 2013. Published November 20, 2013.
Math Subject Classifications: 35J60, 35J35, 35J70.
Key Words: p(x)-Kirchhoff type equations; variational methods;
boundary value problems.
A corrigendum was posted on August 27, 2014. It modifies inequality (3.1), and deletes assumption (M2). This is necessary because there is no function satisying the original assumptions (M1) and (M2). See the last page of this article.
Show me the PDF file (243 KB), TEX file, and other files for this article.
 |
Ghasem Alizadeh Afrouzi Department of Mathematics, Faculty of Mathematical Sciences University of Mazandaran, Babolsar, Iran email: afrouzi@umz.ac.ir |
|---|---|
 |
Maryam Mirzapour Department of Mathematics, Faculty of Mathematical Sciences University of Mazandaran, Babolsar, Iran email mirzapour@stu.umz.ac.ir |
Return to the EJDE web page