Meng-Rong Li, Hsin-Yu Yao, Yu-Tso Li
Abstract:
In this article we study properties of positive solutions
of the ordinary differential equation
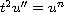 for
for
 ,
we obtain conditions for their blow-up
in finite time, and some properties for global solutions.
Equations containing more general nonlinear terms are also considered.
,
we obtain conditions for their blow-up
in finite time, and some properties for global solutions.
Equations containing more general nonlinear terms are also considered.
Submitted October 5, 2013. Published November 20, 2013.
Math Subject Classifications: 34A34, 34C11, 34C60.
Key Words: Nonlinear differential equation; Emden-Fowler equation; blow-up rate.
Show me the PDF file (208 KB), TEX file, and other files for this article.
 |
Meng-Rong Li Department of Mathematical Sciences National Chengchi University Taipei, Taiwan email: liwei@math.nccu.edu.tw |
|---|---|
| Hsin-Yu Yao Department of Mathematical Sciences National Chengchi University Taipei, Taiwan email: diadia0914@gmail.com | |
| Yu-Tso Li Department of Aerospace and Systems Engineering Feng Chia University Taichung, Taiwan email: joycelion74@gmail.com |
Return to the EJDE web page