We study the existence and asymptotic behavior of self-similar solutions to the parabolic problem
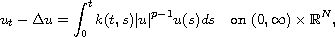
with p>1 and
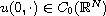 .
.
Miguel Loayza
Abstract:
We study the existence and asymptotic behavior of self-similar
solutions to the parabolic problem
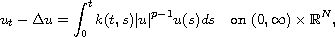
with p>1 and
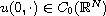 .
.
Submitted August 9, 2012. Published October 16, 2013.
Math Subject Classifications: 35K15, 35B40, 35E15.
Key Words: Nonlocal parabolic equation; global solution;
self-similar solution.
Show me the PDF file (266 KB), TEX file, and other files for this article.
 |
Miguel Loayza Departamento de Matemática Universidade Federal de Pernambuco 50740-540, Recife, PE, Brazil email: miguel@dmat.ufpe.br |
|---|
Return to the EJDE web page