Electron. J. Diff. Equ., Vol. 2013 (2013), No. 222, pp. 1-7.

Energy decay for degenerate Kirchhoff equations with weakly nonlinear dissipation

Mama Abdelli, Salim A. Messaoudi

Abstract:
In this article we consider a degenerate Kirchhoff equation wave equation with a weak frictional damping,
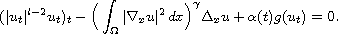
$$ (|u_t|^{l-2}u_t)_t-\Big( \int_{\Omega }|\nabla _x u|^{2}\,dx\Big)^{\gamma } \Delta _xu+\alpha (t)g(u_t)=0. $$
We prove general stability estimates using some properties of convex functions, without imposing any growth condition at the frictional damping term.

Submitted September 18, 2013. Published October 11, 2013.
Math Subject Classifications: 35B37, 35L55, 74D05, 93D15, 93D20.
Key Words: Decay of solutions; nonlinear; degenerate; Kirchhoff equation.

Show me the PDF file (208 KB), TEX file, and other files for this article.

  Mama Abdelli
Université Djillali Liabés, Laboratoire de Mathématique
B.P. 89. Sidi Bel Abbés 22000, Algeria
email: abdelli_mama@yahoo.fr
Salim A. Messaoudi
King Fahd University of Petroleum and Minerals
Department of Mathematics and Statistics
Dhahran 31261, Saudi Arabia
email: messaoud@kfupm.edu.sa

Return to the EJDE web page