Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 220, pp. 1-13.
Anisotropic problems with variable exponents and
constant Dirichlet conditions
Maria-Magdalena Boureanu, Cristian Udrea, Diana-Nicoleta Udrea
Abstract:
We study a general class of anisotropic problems involving
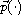 -Laplace
type operators.
We search for weak solutions that are constant on the boundary
by introducing a new subspace of the anisotropic Sobolev space with
variable exponent and by proving that it is a reflexive Banach space.
Our argumentation for the existence of weak solutions is mainly based
on a variant of the mountain pass theorem of Ambrosetti and Rabinowitz.
-Laplace
type operators.
We search for weak solutions that are constant on the boundary
by introducing a new subspace of the anisotropic Sobolev space with
variable exponent and by proving that it is a reflexive Banach space.
Our argumentation for the existence of weak solutions is mainly based
on a variant of the mountain pass theorem of Ambrosetti and Rabinowitz.
Submitted April 8, 2013. Published October 4, 2013.
Math Subject Classifications: 35J25, 46E35, 35D30, 35J20.
Key Words: Anisotropic variable exponent Sobolev spaces;
Dirichlet problem; existence of weak solutions; mountain pass theorem.
A corrigendum was posted on December 23, 2013. It adds a condition to
the original problem, and adds six references. See the last page of this article.
Show me the PDF file (259 KB),
TEX file, and other files for this article.
 |
Maria-Magdalena Boureanu
Department of Applied Mathematics
University of Craiova
200585 Craiova, Romania
email: mmboureanu@yahoo.com
|
|---|
 |
Cristian Udrea
Department of Applied Mathematics
University of Craiova
200585 Craiova, Romania
email: udrea.cristian2013@yahoo.com
|
|---|
 |
Diana-Nicoleta Udrea
Department of Mathematics
University of Craiova
200585 Craiova, Romania
email: diannannicole@yahoo.com
|
|---|
Return to the EJDE web page
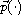 -Laplace
type operators.
We search for weak solutions that are constant on the boundary
by introducing a new subspace of the anisotropic Sobolev space with
variable exponent and by proving that it is a reflexive Banach space.
Our argumentation for the existence of weak solutions is mainly based
on a variant of the mountain pass theorem of Ambrosetti and Rabinowitz.
-Laplace
type operators.
We search for weak solutions that are constant on the boundary
by introducing a new subspace of the anisotropic Sobolev space with
variable exponent and by proving that it is a reflexive Banach space.
Our argumentation for the existence of weak solutions is mainly based
on a variant of the mountain pass theorem of Ambrosetti and Rabinowitz.


