Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 212, pp. 1-21.
Asymptotic behaviour of branches for ground states of elliptic systems
Vladimir Bobkov, Yavdat Il'yasov
Abstract:
We consider the behaviour of solutions to a system of homogeneous
equations with indefinite nonlinearity depending on two parameters
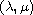 .
Using spectral analysis a critical point
.
Using spectral analysis a critical point
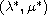 of the Nehari manifolds and fibering methods
is introduced. We study a branch of a ground state and its
asymptotic behaviour, including the blow-up phenomenon at
of the Nehari manifolds and fibering methods
is introduced. We study a branch of a ground state and its
asymptotic behaviour, including the blow-up phenomenon at
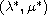 .
.
The differences in the behaviour of similar branches
of solutions for the prototype scalar equations are discussed.
Submitted August 30, 2013. Published September 25, 2013.
Math Subject Classifications: 35J50, 35J55, 35J60, 35J70, 35R05.
Key Words: System of elliptic equations; p-laplacian; indefinite nonlinearity;
Nehari manifold; fibering method.
Show me the PDF file (380 KB),
TEX file, and other files for this article.
 |
Vladimir Bobkov
Institute of Mathematics of RAS, Ufa, Russia
Ufa State Aviation Technical University, Ufa, Russia
email: bobkovve@gmail.com
|
|---|
 |
Yavdat Il'yasov
Institute of Mathematics of RAS, Ufa, Russia
email: ilyasov02@gmail.com
|
|---|
Return to the EJDE web page
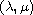 .
Using spectral analysis a critical point
.
Using spectral analysis a critical point
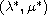 of the Nehari manifolds and fibering methods
is introduced. We study a branch of a ground state and its
asymptotic behaviour, including the blow-up phenomenon at
of the Nehari manifolds and fibering methods
is introduced. We study a branch of a ground state and its
asymptotic behaviour, including the blow-up phenomenon at
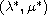 .
.

