Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 209, pp. 1-9.
Boundedness in a chemotaxis system with consumption of
chemoattractant and logistic source
Liangchen Wang, Shahab Ud-Din Khan, Salah Ud-Din Khan
Abstract:
In this article, we consider a chemotaxis system with consumption
of chemoattractant and logistic source
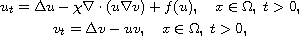
under homogeneous Neumann boundary conditions in a smooth bounded domain
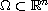 , with non-negative initial data
, with non-negative initial data
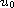 and
and
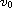 satisfying
satisfying
 (for some
(for some
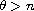 ).
).
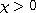 is a parameter referred to as
chemosensitivity and
is a parameter referred to as
chemosensitivity and
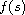 is assumed to generalize the logistic function
is assumed to generalize the logistic function
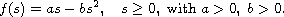
It is proved that if
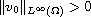 is sufficiently small
then the corresponding initial-boundary value problem possesses a unique
global classical solution that is uniformly bounded.
is sufficiently small
then the corresponding initial-boundary value problem possesses a unique
global classical solution that is uniformly bounded.
Submitted July 1, 2013. Published September 19, 2013.
Math Subject Classifications: 35B35, 35K55, 92C17.
Key Words: Chemotaxis; global existence; boundedness; logistic source.
Show me the PDF file (234 KB),
TEX file, and other files for this article.
 |
Liangchen Wang
College of Mathematics and Statistics
Chongqing University, Chongqing 401331, China
email: liangchenwang324@126.com
|
|---|
 |
Shahab Ud-Din Khan
College of Mathematics and Statistics
Chongqing University, Chongqing 401331, China
email: sudkhan@163.com
|
|---|
 |
Salah Ud-Din Khan
College of Engineering, King Saud University
P.O. Box 800, Riyadh 11421, Kingdom of Saudi Arabia
email: salahudkhan@126.com
|
|---|
Return to the EJDE web page
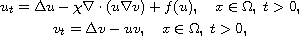
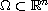 , with non-negative initial data
, with non-negative initial data
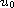 and
and
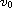 satisfying
satisfying
 (for some
(for some
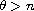 ).
).
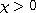 is a parameter referred to as
chemosensitivity and
is a parameter referred to as
chemosensitivity and
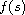 is assumed to generalize the logistic function
is assumed to generalize the logistic function
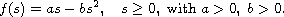
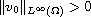 is sufficiently small
then the corresponding initial-boundary value problem possesses a unique
global classical solution that is uniformly bounded.
is sufficiently small
then the corresponding initial-boundary value problem possesses a unique
global classical solution that is uniformly bounded.


