Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 208, pp. 1-13.
Existence and asymptotic behavior of solutions for Henon equations
in hyperbolic spaces
Haiyang He, Wei Wang
Abstract:
In this article, we consider the existence and asymptotic behavior
of solutions for the Henon equation
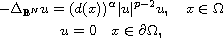
where
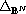 denotes the Laplace Beltrami operator
on the disc model of the Hyperbolic space
denotes the Laplace Beltrami operator
on the disc model of the Hyperbolic space
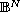 ,
,
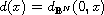 ,
,
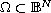 is geodesic ball with radius
is geodesic ball with radius
 ,
,
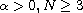 .
We study the existence of hyperbolic symmetric solutions
when
.
We study the existence of hyperbolic symmetric solutions
when
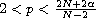 . We also investigate asymptotic
behavior of the ground state solution when p tends to the critical exponent
. We also investigate asymptotic
behavior of the ground state solution when p tends to the critical exponent
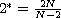 with
with
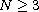 .
.
Submitted May 29, 2013. Published September 19, 2013.
Math Subject Classifications: 35J20, 35J60.
Key Words: Henon equation; hyperbolic space; asymptotic behavior; blow up.
Show me the PDF file (276 KB),
TEX file, and other files for this article.
 |
Haiyang He
College of Mathematics and Computer Science
Key Laboratory of High Performance Computing and
Stochastic Information Processing, Ministry of Education
Hunan Normal University, Changsha, Hunan 410081, China
email: hehy917@hotmail.com
|
|---|
 |
Wei Wang
College of Mathematics and Computer Science
Key Laboratory of High Performance Computing and
Stochastic Information Processing, Ministry of Education
Hunan Normal University, Changsha, Hunan 410081, China
email: ww224182255@sina.com
|
|---|
Return to the EJDE web page
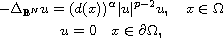
 denotes the Laplace Beltrami operator
on the disc model of the Hyperbolic space
denotes the Laplace Beltrami operator
on the disc model of the Hyperbolic space
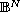 ,
,
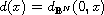 ,
,
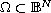 is geodesic ball with radius
is geodesic ball with radius
 ,
,
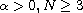 .
We study the existence of hyperbolic symmetric solutions
when
.
We study the existence of hyperbolic symmetric solutions
when
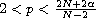 . We also investigate asymptotic
behavior of the ground state solution when p tends to the critical exponent
. We also investigate asymptotic
behavior of the ground state solution when p tends to the critical exponent
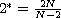 with
with
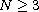 .
.

