Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 207, pp. 1-9.
Multiple solutions for semilinear elliptic equations with
sign-changing potential and nonlinearity
Dongdong Qin, Xianhua Tang, Jiang Zhang
Abstract:
In this article, we study the multiplicity of solutions
for the semilinear elliptic equation
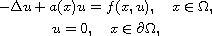
where
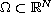
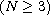 , the potential a(x)
satisfies suitable integrability conditions, and the primitive of
the nonlinearity f is of super-quadratic growth near infinity
and is allowed to change sign. Our super-quadratic conditions are weaker
the usual super-quadratic conditions.
, the potential a(x)
satisfies suitable integrability conditions, and the primitive of
the nonlinearity f is of super-quadratic growth near infinity
and is allowed to change sign. Our super-quadratic conditions are weaker
the usual super-quadratic conditions.
Submitted April 22, 2013. Published September 18, 2013.
Math Subject Classifications: 35J25, 35J60, 58E05.
Key Words: Semilinear elliptic equation; super-quadratic;
sign-changing potential.
Show me the PDF file (226 KB),
TEX file, and other files for this article.
 |
Dongdong Qin
School of Mathematics and Statistics, Central South University
Changsha, 410083 Hunan, China
email: qindd132@163.com
|
|---|
 |
Xianhua Tang
School of Mathematics and Statistics, Central South University
Changsha, 410083 Hunan, China
email: tangxh@mail.csu.edu.cn
|
|---|
 |
Jiang Zhang
School of Mathematics and Statistics, Central South University
Changsha, 410083 Hunan, China
email: zhangjian433130@163.com
|
|---|
Return to the EJDE web page
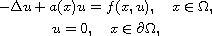
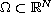
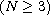 , the potential a(x)
satisfies suitable integrability conditions, and the primitive of
the nonlinearity f is of super-quadratic growth near infinity
and is allowed to change sign. Our super-quadratic conditions are weaker
the usual super-quadratic conditions.
, the potential a(x)
satisfies suitable integrability conditions, and the primitive of
the nonlinearity f is of super-quadratic growth near infinity
and is allowed to change sign. Our super-quadratic conditions are weaker
the usual super-quadratic conditions.


