Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 205, pp. 1-9.
Periodic solutions for fourth-order p-Laplacian functional
differential equations with sign-variable coefficient
Jiaying Liu, Wenbin Liu, Bingzhuo Liu
Abstract:
Using the theory of coincidence degree, we show the
existence of periodic solutions to the fourth-order
p-Laplacian differential equations of Lienard-type
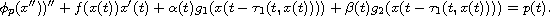
The rate of growth of
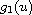 with respect to the variable
u is allowed to be greater than p-1, and the coefficient
with respect to the variable
u is allowed to be greater than p-1, and the coefficient
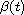 is allowed to change sign.
is allowed to change sign.
Submitted October 7, 2012. Published September 18, 2013.
Math Subject Classifications: 34A12, 34C25.
Key Words: p-Laplacian equation; periodic solution;
multiple deviating argument; Mawhin continuation theorem.
Show me the PDF file (202 KB),
TEX file, and other files for this article.
 |
Jiaying Liu
Department of Mathematics
China University of Mining and Technology
Xuzhou, Jiangsu 221116, China
email: relinaliu@163.com
|
|---|
 |
Wenbin Liu
Department of Mathematics
China University of Mining and Technology
Xuzhou, Jiangsu 221116, China
email: wblium@163.com
|
|---|
 |
Bingzhuo Liu
Department of Mathematics
China University of Mining and Technology
Xuzhou, Jiangsu 221116, China
email: tuteng3839@163.com
|
|---|
Return to the EJDE web page
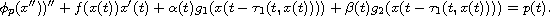
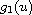 with respect to the variable
u is allowed to be greater than p-1, and the coefficient
with respect to the variable
u is allowed to be greater than p-1, and the coefficient
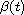 is allowed to change sign.
is allowed to change sign.


