Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 196, pp. 1-28.
Stokes problem with several types of boundary conditions in an exterior domain
Cherif Amrouche, Mohamed Meslameni
Abstract:
In this article, we solve the Stokes problem in an exterior domain of
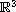 ,
with non-standard boundary conditions.
Our approach uses weighted Sobolev spaces to
prove the existence, uniqueness of weak and strong solutions.
This work is based on the vector potentials studied in [7]
for exterior domains, and in [1] for bounded domains.
This problem is well known in the classical Sobolev spaces
,
with non-standard boundary conditions.
Our approach uses weighted Sobolev spaces to
prove the existence, uniqueness of weak and strong solutions.
This work is based on the vector potentials studied in [7]
for exterior domains, and in [1] for bounded domains.
This problem is well known in the classical Sobolev spaces
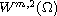 when
when
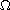 is bounded; see [3,4].
is bounded; see [3,4].
Submitted July 28, 2013. Published September 3, 2013.
Math Subject Classifications: 35J25, 35J50, 76M30.
Key Words: Stokes equations; exterior domain; weighted Sobolev spaces;
vector potentials; inf-sup conditions.
Show me the PDF file (400 KB),
TEX file, and other files for this article.
 |
Chérif Amrouche
Laboratoire de Mathématiques et de leurs Applications
Pau - CNRS UMR 5142,
Université de Pau et des Pays de l'Adour
IPRA, Avenue de l'Université - 64000 Pau - France
email: cherif.amrouche@univ-pau.fr
|
|---|
| |
Mohamed Meslameni
Laboratoire de Mathématiques et de leurs Applications
Pau - CNRS UMR 5142,
Université de Pau et des Pays de l'Adour
IPRA, Avenue de l'Université - 64000 Pau - France
email: mohamed.meslameni@univ-pau.fr
|
|---|
Return to the EJDE web page
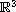 ,
with non-standard boundary conditions.
Our approach uses weighted Sobolev spaces to
prove the existence, uniqueness of weak and strong solutions.
This work is based on the vector potentials studied in [7]
for exterior domains, and in [1] for bounded domains.
This problem is well known in the classical Sobolev spaces
,
with non-standard boundary conditions.
Our approach uses weighted Sobolev spaces to
prove the existence, uniqueness of weak and strong solutions.
This work is based on the vector potentials studied in [7]
for exterior domains, and in [1] for bounded domains.
This problem is well known in the classical Sobolev spaces
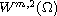 when
when
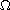 is bounded; see [3,4].
is bounded; see [3,4].
