Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 182, pp. 1-16.
Reconstructing the potential function for indefinite
Sturm-Liouville problems using infinite product forms
Mohammad Dehghan, Ali Asghar Jodayree
Abstract:
In this article we consider the linear second-order equation of
Sturm-Liouville type
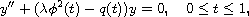
where
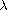 is a real parameter,
is a real parameter,
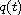 is the potential function
and
is the potential function
and
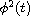 is the weight function. We use the infinite product
representation of the derivative of the solution to the differential equation
with Dirichlet-Neumann conditions, and for the system of dual equations
which is needed for expressing inverse problem and for retrieving potential.
It must be mentioned that the weight function has a zero whose order
is an integer called a turning point.
is the weight function. We use the infinite product
representation of the derivative of the solution to the differential equation
with Dirichlet-Neumann conditions, and for the system of dual equations
which is needed for expressing inverse problem and for retrieving potential.
It must be mentioned that the weight function has a zero whose order
is an integer called a turning point.
Submitted July 15, 2013. Published August 7, 2013.
Math Subject Classifications: 34B24, 34A55, 34E20, 34E05.
Key Words: Indefinite Sturm-Liouville problem; turning point; dual equations;
infinite product form.
Show me the PDF file (288 KB),
TEX file, and other files for this article.
 |
Mohammad Dehghan
Faculty of Mathematical Sciences
University of Tabriz
Tabriz, Iran
email: m-dehghan@tabrizu.ac.ir, Tel. +989113512619
|
|---|
 |
Ali Asghar Jodayree
Faculty of Mathematical Sciences
University of Tabriz
Tabriz, Iran
email: akbarfam@yahoo.com
|
|---|
Return to the EJDE web page
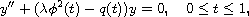
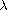 is a real parameter,
is a real parameter,
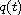 is the potential function
and
is the potential function
and
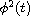 is the weight function. We use the infinite product
representation of the derivative of the solution to the differential equation
with Dirichlet-Neumann conditions, and for the system of dual equations
which is needed for expressing inverse problem and for retrieving potential.
It must be mentioned that the weight function has a zero whose order
is an integer called a turning point.
is the weight function. We use the infinite product
representation of the derivative of the solution to the differential equation
with Dirichlet-Neumann conditions, and for the system of dual equations
which is needed for expressing inverse problem and for retrieving potential.
It must be mentioned that the weight function has a zero whose order
is an integer called a turning point.

