Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 179, pp. 1-14.
Exponential stability of traveling fronts for a 2D lattice
delayed differential equation with global interaction
Shi-Liang Wu, Tian-Tian Liu
Abstract:
The purpose of this paper is to study traveling wave fronts of a
two-dimensional (2D) lattice delayed differential equation with global
interaction. Applying the comparison principle combined with the
technical weighted-energy method, we prove that any given traveling wave
front with large speed is time-asymptotically stable when the initial
perturbation around the wave front need decay to zero exponentially as
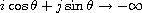 , where
, where
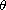 is
the direction of propagation, but it can be allowed relatively large in
other locations. The result essentially extends the stability of traveling
wave fronts for local delayed lattice differential equations obtained
by Cheng et al [1] and Yu and Ruan [16].
is
the direction of propagation, but it can be allowed relatively large in
other locations. The result essentially extends the stability of traveling
wave fronts for local delayed lattice differential equations obtained
by Cheng et al [1] and Yu and Ruan [16].
Submitted July 1, 2013. Published August 4, 2013.
Math Subject Classifications: 35K57, 35R10, 35B40, 92D25.
Key Words: Exponential stability; traveling wave front; global interaction;
lattice differential equation; comparison principle;
weighted energy method.
Show me the PDF file (245 KB),
TEX file, and other files for this article.
 |
Shi-Liang Wu
Department of Mathematics, Xidian University
Xi'an, Shaanxi 710071, China
email: slwu@xidian.edu.cn
|
|---|
 |
Tian-Tian Liu
Department of Mathematics, Xidian University
Xi'an, Shaanxi 710071, China
email: ahtian4402@qq.com
|
|---|
Return to the EJDE web page
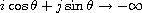 , where
, where
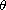 is
the direction of propagation, but it can be allowed relatively large in
other locations. The result essentially extends the stability of traveling
wave fronts for local delayed lattice differential equations obtained
by Cheng et al [1] and Yu and Ruan [16].
is
the direction of propagation, but it can be allowed relatively large in
other locations. The result essentially extends the stability of traveling
wave fronts for local delayed lattice differential equations obtained
by Cheng et al [1] and Yu and Ruan [16].

