Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 174, pp. 1-11.
Uniqueness of positive solutions for fractional q-difference
boundary-value problems with p-Laplacian operator
Fenghua Miao, Sihua Liang
Abstract:
In this article, we study the fractional q-difference boundary-value
problems with p-Laplacian operator

where
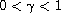 ,
,
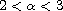 ,
,
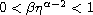 ,
,
 is the
Riemann-Liouville fractional derivative,
is the
Riemann-Liouville fractional derivative,
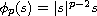 ,
p>1. By using a fixed-point theorem in partially ordered sets, we
obtain sufficient conditions for the existence and uniqueness of
positive and nondecreasing solutions.
,
p>1. By using a fixed-point theorem in partially ordered sets, we
obtain sufficient conditions for the existence and uniqueness of
positive and nondecreasing solutions.
Submitted June 15, 2013. Published July 29, 2013.
Math Subject Classifications: 39A13, 34B18, 34A08.
Key Words: Fractional q-difference equations; partially ordered sets;
fixed-point theorem; positive solution.
Show me the PDF file (237 KB),
TEX file, and other files for this article.
 |
Fenghua Miao
College of Mathematics, Changchun Normal University
Changchun 130032, Jilin, China
email: mathfhmiao@163.com
|
|---|
 |
Sihua Liang
College of Mathematics, Changchun Normal University
Changchun 130032, Jilin, China
email: liangsihua@163.com, Phone 08613578905216
|
|---|
Return to the EJDE web page

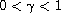 ,
,
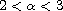 ,
,
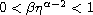 ,
,
 is the
Riemann-Liouville fractional derivative,
is the
Riemann-Liouville fractional derivative,
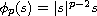 ,
p>1. By using a fixed-point theorem in partially ordered sets, we
obtain sufficient conditions for the existence and uniqueness of
positive and nondecreasing solutions.
,
p>1. By using a fixed-point theorem in partially ordered sets, we
obtain sufficient conditions for the existence and uniqueness of
positive and nondecreasing solutions.

